|
1. Introduction of the conjecture
We assume that the reader is acquainted with the previous article [1] which has introduced the concept of a Generalized Heronian mean Her(k,a) of rank k of an n-tuple a = {a1,a2,...,an} of non-negative real numbers.
In Section 5 of [1], the value Her(k,a) has been expressed as
(1) 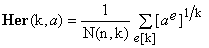 , ,
where N(n,k), equal to the combinatorial coefficient C(n+k-1,k), is the number of all decompositions of the integer number k > 0 into n non-negative integers ei such that
(2)  . .
We are also using the notation introduced in [1] by which
(3) 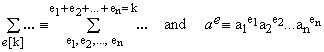
We want to prove that, regardless of the values of n and k,
(4)  . .
2. The proof
From Eq.(1) it transpires that Her(k,a) is simply the arithmetic mean of the N(n,k) distinct terms [ae]1/k. Applying the well-known fact that the arithmetic mean of any set of non-negative real numbers is never smaller than their geometric mean (see [2] and references therein), we obtain
(5) 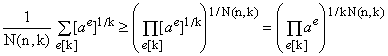
Consider now the product in the last parenthesis on the right. Its factors are all possible expressions of the type shown in Eq.(3). Since in each such expression the sum of all exponents equals k and there are N(n,k) expressions, the result is the product of all ai in which the sum of all exponents is k.N(n,k). Moreover, it is evident that the final product is invariant under any permutation of the indices of the ai's, which implies that it contains each ai elevated to the same power k.N(n,k)/n. Consequently,
(6) 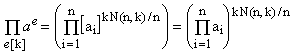
which, substituted into (5), gives the desired result and completes the proof.
Summary
The proof is based on the inequality between the arithmetic mean and the geometric mean, combined with a simple book-keeping of the powers of each element ai in the grand product of Eq.(6). The idea, once grasped, permits to prove on just a few lines one of the conjectures introduced in [1].
From the proof it is evident that inequality (4) is sharp unless all the elements of a are the same. The inequality in (5) in fact becomes equality only when all the terms - and therefore all the products ae - have the same value which is possible only iff all ai are equal.
There remains the conjecture that, keeping a fixed and increasing the value of the rank k, the Heronian means Her(k,a) form a decreasing series. This seems for the moment considerably more difficult to prove than inequality (4), even though it has been already proved [3] for k = 1,2 (any n) and for n = 2 (any k).
|