1. Introduction

We assume that the reader is acquainted with basic definitions and properties [1] pertinent to means, intended as particular types of mathematical mappings of the sets of n-tuples of real numbers belonging to a domain D into the domain itself. In the present case, the domain D is that of all positive real numbers R₊. We assume further that the reader is acquainted with the previous article [2] which has introduced the concept of generalized Heronian means and the articles [3,4] which discuss some their properties.

Reference [2, Section 5] defines the generalized Heronian mean Her(k,a) of rank k of an arbitrary n-tuple a = {a₁,a₂,...,a_n} of non-negative real numbers as follows:

(1)   

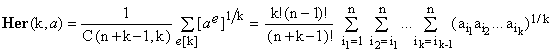
where the normalizing combinatorial coefficient C(n+k-1,k), equals the number of all decompositions of the integer number k > 0 into n non-negative integers e_i such that, using the notation introduced in [2],

(2)   

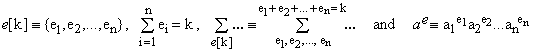
Reference [2] also introduced the concept of the Hermean Her(a) of a, defined as the limit of Her(k,a), for k growing to infinity.

(3)   

The existence of such a limit, however, has been only conjectured and no general expression for its value has been given.
This Note fills the gap, proving that the conjecture has been correct and providing an explicit expression for Her(a).

Just before making this Note public I came across the work of Seppo Mustonen [5], Jorma Merikoski et al who address what I have called Hermean under the designation of the logarithmic mean for several arguments or the generalized logarithmic mean. The two approaches have dissimilar starting points and follow different paths. For one thing, the approach expounded here and in the preceding Notes stems from the generic postulates of a mean, generalizes the algebraic formula for Heronian mean to any number of elements, applies a limit transition, and only subsequently arrives at discovering the connection between the limit on one side and the generalized logarithmic mean on the other side. The approach of Mustonen has as its cardinal point the mean value for divided differences [6,7] of the differential calculus and his principal tool consists in a series expansion of the logarithmic mean L(a,b) in terms of the logarithms ln(a), ln(b) of its arguments and a subsequent generalization of the expansion to any number of arguments. Despite these differences, the two approaches meet at several points and arrive at the same conclusions, reinforcing each other. I believe that the present approach is technically more elementary, in the sense that it relies only on algebraic manipulations and on an elementary limit formula, with no differential calculus. For these reasons, I have decided to go on with the publication, inserting appropriate comparative references to the work of Mustonen and those cited by him.

2. Special cases for n = 1, 2 and 3

For n = 1 we have, compatibly with the general properties of means [1],

(4)   Her(k,{a}) = a,

independently of k. Consequently, Her({a}) exists and equals a.

For n = 2 and a = {a,b}, definition [1] amounts to

(5)   

for which a limit transition exists (see Appendix A3 and A4) and evaluates to

(6)   

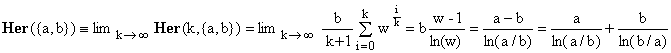
For n = 3 and a = {a,b,c}, definition [1] gives

(7)   

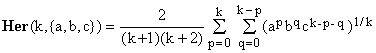
Setting A = a/c, B = b/c, and C = A/B = a/b, this evaluates to

(8)   

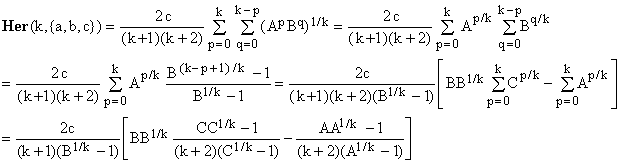
According to (A4) this again admits a limit and

(9)   

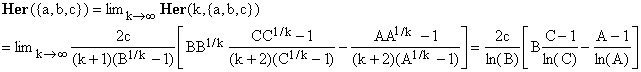
which, after some more manipulation, can be cast as

(10)   

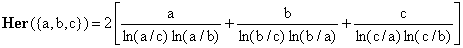
3. An explicit, general formula ...

Inspecting Eqs.(4,6,10) and remembering that (i) Hermean, if it exists at all, is a mean [see 2] and (ii) any mean is invariant under the permutations of the elements of its argument set a, one does not need any particular intuition to guess that a general formula for Her(a), with a = {a₁,a₂,...,a_n}, could be

(11)   

This matches all the special cases discussed above, provided that when n = 1, the empty product in the denominator on the right-hand-side is conventionally interpreted as 1.

Equation (11) matches Mustonen's [5, Eq.4] for his generalized logarithmic mean. It has been apparently conjectured by him in an unpublished manuscript already in 1976. For him, however, the starting point is the extension of a series expansion for the generalized logarithmic mean. He derives the expression as a closed form solution for the said series, while here it is interpreted as a limit of a sequence of quantities already known to be means.

4. ... and its proof

Since Eq.(11) has been proved for n = 1,2 and 3, we will now proceed by induction, assuming that it holds up to some (n) and showing that this implies its validity for (n+1). For this purpose we will intend a as a set of (n+1) elements, a = {a₁,a₂,...,a_n+1} and, consequently, the set e = {e₁,e₂,...,e_n+1} as a decomposition of k into (n+1) non-negative integers. Definition (1) in this case gives

(12)   

where, in the second part, we have "normalized" all the elements of a dividing them by a_n+1 which was brought in front.

We now define a new quantity, namely F(k,a):

(13)   

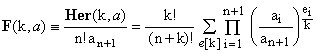
Obviously, the last factor in the product, being a power of 1, is identically one, regardless of its exponent e_n+1/k.
F(k,a) can be therefore rewritten as follows:

(14)   

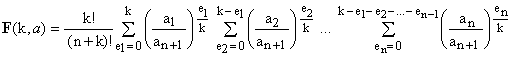
The last factor in (14) is a finite geometric series and, though the expressions look cumbersome, can be easily summed:

(15)   

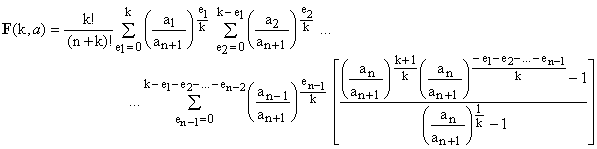
which can be further re-arranged as

(16)   

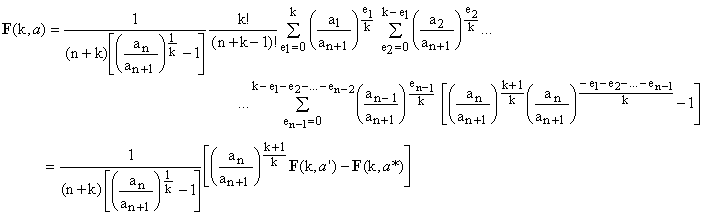
In the last passage, we have introduced two sets of (n) elements, a' and a* derived from the set a of (n+1) elements as follows:

(17)   a = {a₁,a₂,...,a_n-1,a_n,a_n+1}   →   a' = {a₁,a₂,...,a_n-1,a_n}, a* = {a₁,a₂,...,a_n-1,a_n+1}

Substituting back into Eq.(16) the expressions for F(k,a), we now obtain

(18)   

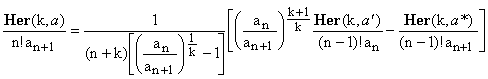
which, after a small re-arrangement, gives an interesting recurrence relation for Her(k,a):

(19)   

By assumption, the limits for Her(k,a') and Her(k,a*) exist. Hence, in virtue of (A4), the limit of Her(k,a) exists as well and

(20)   

or, equivalently,

(21)   

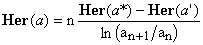
Having proved the existence of the limit, it remains to be shown that the recurrence (20) is compatible with Eq.(11).

In order to do so, let us substitute Her(k,a') and Her(k,a*) es defined by Eq.(11) into the RHS of Eq.(21), properly adjusted for a' and a*, and see whether we recover the expression for Her(k,a) implicit in the LHS.
The algebra, somewhat complicated, spins out as follows:

First, we have

(22)   

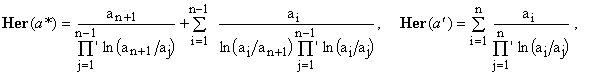
where the apostrophes over the product symbols indicate that factors containing elements with the same indices are to be skipped. Substituting Eqs.(22) into the RHS of Eq.(21), its value becomes

(23)   

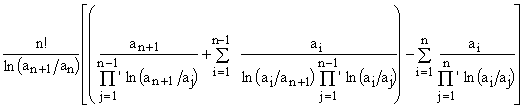
Now, splitting off the last term in the rightmost summation, we get

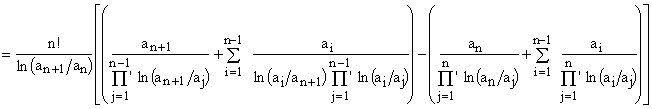
which can be rearranged as

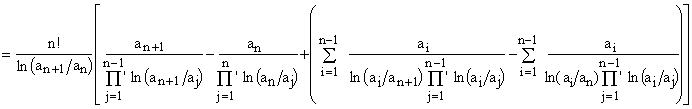
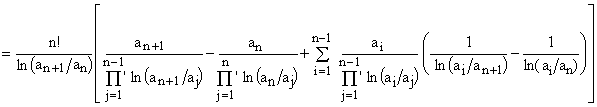
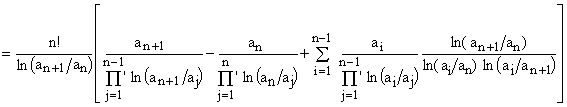
and finally simplified to

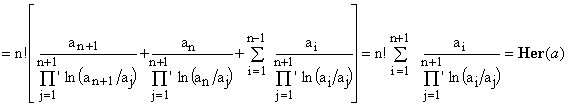
We thus see that the final form of the RHS of Eq.(21) is indeed identical to Eq.(11) when applied to the (n+1)-elements set a.
QED.

5. Checking special cases

After such complicated algebraic manipulations it is always pleasing to check the validity of the result.
For a = {a,b}, for example, we have a' = {a} and a* = {b} and Eq.(21) gives the expected form

(24)   

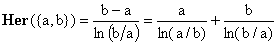
For a = {a,b,c} we have a' = {a,b} and a* = {a,c} and Eq.(21) gives

(25)   

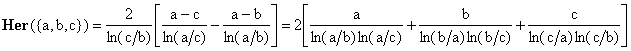
which is the same as Eq.(10).

6. Some properties of the Hermean

To avoid any confusion, let us agree that from now on, unless specified otherwise, a will be again a set of (n) positive real numbers, a = {a₁,a₂,...,a_n}.

The Hermean, being a limit case of a progression of means, is itself a mean and satisfies all the respective postulates [1]. In particular, Her(a) is invariant under any permutation of the elements of a, it scales in a linear way, i.e., Her(ca) = c. Her(a), and

(26)   .

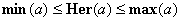The latter inequality is hardly immediately apparent from Eq.(11). It is the body of deductions contained in this Note, jointly with the preceding ones [1,2], that constitutes its proof.

Applying the limit transition to the inequality proved in [4], we see also that Her(a) can not be smaller that the geometric mean G(a) of the elements of a. Since this is a stronger condition than the one in (26), we can sum up the proved inequalities as

(27)   .

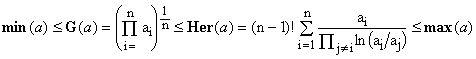Several upper-limit inequalities for Her(a) sharper than the max(a) bound are very likely to hold, even though a rigorous and general proof is still missing. These stem from the conjecture [1] that the progression Her(k,a), k = 1, 2, 3, ..., is non-increasing, regardless of a. Since Her(1,a) = A(a) is the arithmetic mean of a, this would imply the following conjectured inequalities, so far rigorously proved only for n = 2 [3, Section 3], but extensively tested [1] by numerical methods:

(28)   .

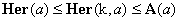The inequalities G(a) ≤ Her(a) ≤ A(a) appear also in Mustonen [5] and in some of the references cited by him.

Let us now re-consider Eq.(21). Due to the permutation symmetry of Her(a), it leads directly to the following identities:
Let a = {a₁,a₂,...,a_n} and denote as a^(p) the set obtained from a by dropping its element with index p (meaning a_p).
Then when p and q are two distinct indices, we obtain a more generic recurrence formula:

(29)   .

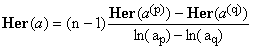From this it also follows that when r and s is another pair of distinct indices (not necessarily both distinct from p and q), then

(30)   .

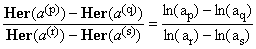A word must be said about those cases when two or more of the elements of a coincide. From the definition of Her(k,a) in Eq.(1) and that of Her(a) as its limit, it is clear that such coalescence cases do NOT constitute any singularities, while Eq.(11) apparently contradicts this fact. The problem is indeed just apparent and resolves itself replacing those values of Eq.(11) which might be undefined due to coalescence with suitable limit values. Intended as a function of n variables, Her(a) is everywhere continuous and smooth (i.e., possesses derivatives of any order), notwithstanding the functional form of Eq.(11). It is true, however, that evaluation of Her(a) by means of Eq.(11) can in cases of coalescence represent a problem and special algorithms are called for to avoid numeric instabilities.

Another property which can be ascertained only by means of limit transitions, regards the behavior of Her(a) when any of the elements of a tends to zero. It can be easily proved that in this case Her(a) also tends to zero, just like G(a). This permits us to extend the definition of Her(a) to sets a of any non-negative real elements, even though Eq.(11) seemingly fails when an element becomes zero.

The above features are closely related to the fact that as far as computational efficiency is concerned, Hermean is neither thrifty nor efficient (for definitions, see [1]). As mentioned by Mustonen [5], equation (11) is numerically very unstable. The algorithm for Her(k,a) described in reference [2], Section 4, is suitable for small k, but far from efficient for k growing to infinity and it is not quite clear at this moment whether the series-expansion method of Mustonen [5] might be more efficient or not. Pending future improvements, this probably limits the practical usefulness of Hermeans.

7. Related concepts

For two elements {a,b} the Hermean coincides with what is known as the logarithmic mean [5], so that Her(a) and Eq.(11) can be considered as extensions thereof to any number of elements. The logarithmic mean arises in many situations where a quantity depends inversely upon a metric parameter r (radius) and must be integrated between the limits {a,b} imposed upon r. In a sense, the value of Her({a,b}) can be interpreted as the harmonic mean value of r:

(31)   

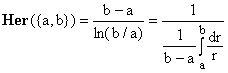
This interpretation, however, does not seem to extend easily to more than two elements.

APPENDIX

Let us list here some of the rather elementary limits used above. Given any positive real numbers x and p, the first one is

(A1)   ,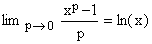

the proof of which is best done by applying the l'Hospital rule. Replacing x by 1/k, with a positive integer k, this gives

(A2)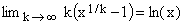   

Finally, one can apply this to the average of the first k terms of a geometric series, obtaining

(A3)   .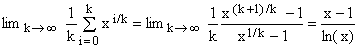

Notice that the singularity of the right-hand-side at x = 1 is only apparent; both sides have in fact a well defined limit (equal to 1) and the function (x-1)/ln(x) is perfectly smooth (i.e., all its derivatives exist and are finite) at x = 1.

A most general form of (A3), readily proved, is valid for any non-negative constant integers p,q and any positive real r:

(A4) 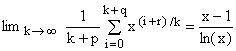  .