|
1. Introduction
In this Note we focus our attention on a class of surface integrals over n-dimensional real spheres which can be evaluated explicitly. We postpone the evaluation of surface integrals over generic ellipsoids because they involve transcendental elliptic integrals.
Like in [1], let Rn denote the n-dimensional Euclidean space, r the position vector in Rn and r = |r| its norm
(1) 
where the x's are its Cartesian coordinates. We shall often use n-tuples of non-negative real exponents
(2) 
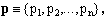
which, however, are not to be intended as elements of Rn.
The shorthand will be exploited in conventional expressions of the type
(3) 
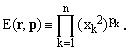
In this notation, an n-dimensional spherical surface S(R) of radius R is defined by the condition
(4) 
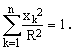
We are interested in the evaluation of the following integrals over S(R):
(5) 
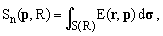
where dσ is an (n-1)-dimensional surface element.
2. Evaluation of the integrals
Evaluation of the integrals (5) is considerably simplified by three facts:
a) From reference [1], Equation 17, we know the value of the corresponding volume integral over the n-dimensional sphere, which turns out to be
(6) 
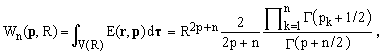
where Γ(x) denotes the gamma function [4,5].
b) Integrals (5) have the nearly self-evident scaling property
(7) 
arising from the fact that E(r,p) scales with 2p-th power of R and dσ scales with (n-1)-st power or R.
c) For spheres (unlike generic ellipsoids), the volume integration can be carried out by summing the contributions of concentric shells defined by radii r and r+dr, for r ranging from 0 to R. Hence
(8) 
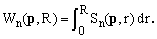
From (8) and (7) it follows that
(9) 
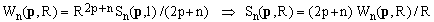
from which, comparing with (6), we obtain the result
(10) 
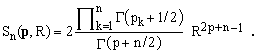
In the original paper [3] which stimulated this series of Notes, formula (10) was derived in a more direct - and also more laborious - way. It is therefore pleasing to note that the two procedures lead to the same result.
3. Admissible values of the exponents (p's)
For reasons discussed in [1], the values of pk may assume any real value greater than -1/2, which are also the values compatible with Equation (10). Moreover, one should keep in mind that in equations (3) and (5), the individual Cartesian coordinates xk get first squared and only afterwards elevated to pk. Thus, for example, when pk = -1/4, the corresponding factor in Eq.(3) is the square root of |xk|.
4. Special cases
Setting all the p's equal to ν/2, one obtains the following formula, valid for any ν>-1:
(11) 
In particular, setting ν = 1 and taking into account that Γ(n) = (n-1)!, we obtain the formula
(12) 
When only one of the p's equals ν/2 and all the others are zero, Eq.(10) yields the identity, again valid for any ν>-1:
(13) 
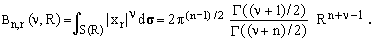
For the important cases of ν=1 and ν=2, this gives
(14) 
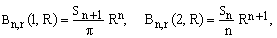
where
(15) 
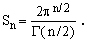
5. Surfaces of n-dimensional spheres
When all the p's are zero, Eq.(10) gives simply the surface of the n-dimensional sphere. Explicitly, this turns out to be
(16) 
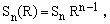
showing that the the numbers Sn of Eq.(22) are the surfaces of n-dimensional spheres of unit radius whose values can be easily calculated by means of the recurrence
(17) 
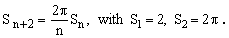
The surface of an n-dimensional sphere has the dimension of the (n-1)-st power of length. This coincides with the popular notion of "surface area" only in the case of n=3 but its extension to any n is quite obvious. In particular, for n=2 it coincides with the common concept of "circumference" of a circle. The value of 2 for n=1, implicit in the above recurrence relations, can be considered as the cardinality of the set of the two end points of a 1D interval.
Surfaces and other surface integrals for n-dimensional spheres with unit radius
| |
| Dim |
Surface |
|
Surface integral of: |
| symbolic |
numeric |
|
|x1| |
x12 |
|x1x2| |
x12x22 |
| |
| 1 |
2 |
2.000000.. |
|
2 |
2 |
- |
- |
| 2 |
2π |
6.283185.. |
|
4 |
π |
2 |
π/4 |
| 3 |
4π |
12.566370.. |
|
2π |
4π/3 |
8/3 |
4π/15 |
| 4 |
2π2 |
19.739208.. |
|
8π/3 |
π2/2 |
π |
π2/12 |
| 5 |
8π2/3 |
26.318945.. |
|
π2 |
8π2/15 |
16π/15 |
8π2/105 |
| 6 |
π3 |
31.006276.. |
|
16π2/15 |
π3/6 |
π2/3 |
π3/48 |
| 7 |
16π3/15 |
33.073361.. |
|
π3/3 |
16π3/105 |
32π2/105 |
16π3/1185 |
| 8 |
π4/3 |
32.469697.. |
|
32π3/105 |
π4/24 |
π3/12 |
π4/240 |
| 9 |
32π4/105 |
29.686580.. |
|
π4/12 |
32π4/945 |
64π3/945 |
32π4/10395 |
| 10 |
π5/12 |
25.501640.. |
|
64π4/945 |
π5/120 |
π4/60 |
π5/1440 |
| |
Note: Numerically, the surface integral of x12 over a unit sphere equals its volume.
6. Asymptotic behavior
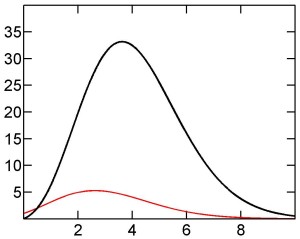Equation (15) for the surface of an n-dimensional sphere of unit radius can be rewritten in terms of the following function σ(x):
(18) 
whose graph is shown on the right (bold black line), together with the analogous function ν(x) for unit sphere volumes (thin red line). The relation between the two functions is σ(x) = 2x.ν(x).
It is evident that both functions pass through a maximum and then, for large x, decay rapidly to zero. A very good approximation for the logarithms of both functions can be obtained by a straightforward application of Stirling formula [4,5] for ln(Γ(x)).
The asymptotic behavior is rather complicated. Roughly, one can affirm that, for very large x, the decay of both functions is dominated by a factor of the form O[x-x].
|