|
1. Introduction
We will focus our attention on certain classes of volume integrals over n-dimensional real ellipsoids which, as we shall see, can be integrated explicitly. For the moment we postpone the evaluation of surface integrals because they are much more difficult to handle. In the simple case of two-dimensions, for example, the area of an elipsis is given by the explicit formula πab (a,b being the two semiaxes), while its circumference involves transcendental elliptic integrals. There is a relationship between the two categories, however, so the effort needed to analyse volume integrals will not be lost.
Let Rn denote the n-dimensional Euclidean space. The position vector r and its norm r = |r| of a point in Rn and its norm r can be written as
(1) 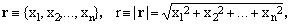
where the x's are its Cartesian coordinates. We shall often use n-tuples of non-negative real exponents
(2) 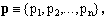
which, however, are not to be intended as elements of Rn. The shorthand will be exploited in conventional expressions of the type
(3) 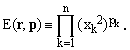
In addition, n-tuples of semi-axes
(4) 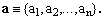
will be used to define ellipsoid volumes V(a) in Rn by means of the condition
(5) 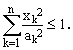
This implies that the ellipsoid axes are aligned with the Cartesian axes and that, for the sake of uniqueness, all the a's should be non-negative. We shall be interested in the evaluation and analysis of the following integrals over ellipsoid volumes V(a):
(6) 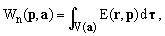
where dτ is the volume element.
2. Evaluation of the integrals
In Cartesian coordinates, the volume element dτ is given by
(7) 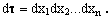
Applying the coordinates-scaling transformation
(8) 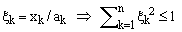
one obtains
(9) 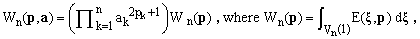
with Vn(R) denoting the interior of an n-dimensional sphere of radius R (in this case, R=1).
To compute the last integral in (9), we can proceed iteratively, reducing the dimensionality of the problem by 1 in each step. The setting
(10) 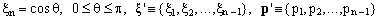
corresponds to a cut of the n-dimensional sphere at a value of the last coordinate given by the cosine of the polar angle θ. Considering the inequality in (8), we see that the cut is an (n-1)-dimensional sphere of radius R = sinθ, so that
(11) 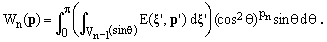
An (n-1)-dimensional sphere of radius R is an ellipsoid whose semi-axes set a' has all components equal to R. Hence, using Eq.(9),
(12) 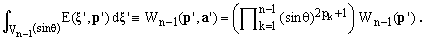
Substituting the last equation into (11), one obtains
(13) 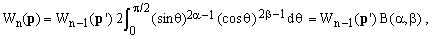
where B(α,β) is the beta function [4,5] and
(14) 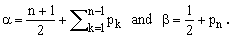
The beta function can be expressed by means of the gamma function [4,5] which leads to
(15) 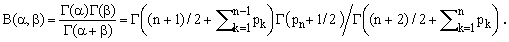
The starting term (for n=1) in the recurrence (13) is easily determined by explicit integration (it can be also shown that the recurrence is compatible with the formal assumption according to which a zero-dimensional unit sphere has volume 1). Using the recurrence and applying repetitively Eq.(15), it is straightforward to determine that
(16) 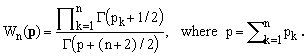
Combining this with Eq.(9) and taking advantage of the fact that Γ(z+1) = zΓ(z), we finally obtain the following closed-form expression for the desired integral over an ellipsoidal volume
(17) 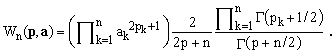
3. Admissible values of the exponents (p's)
In equations (3), (6) and (11) we have made it clear that an individual Cartesian coordinate xk get first squared and only afterwards elevated to pk (this fact is essential also in the passage from II.5 to II.7). Consequently, the values of pk are not limited to natural integers and zero but may assume any real value greater than -1/2 , a bound due to the fact that the α and β in Eq.(13) must be positive for the beta function definition to hold.
4. Special cases
Setting all the p's equal to ν/2, one obtains the following formula, valid for any ν>-1:
(18) 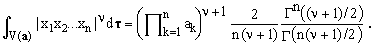
In particular, setting ν = 1 and taking into account that Γ(1) = 1, we obtain the interesting formula
(19) 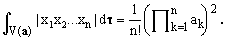
Notice that for n-dimensional spheres of unit radius, the right-hand side of this identity reduces to 1/n!.
When only one of the p's equals ν/2 and all the others are zero, Eq.(17) yields the identity, again valid for any ν>-1:
(20) 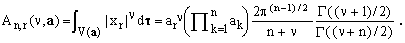
For the important cases of ν=1 and ν=2, this gives
(21) 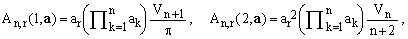
where
(22) 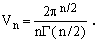
Finally, summing over all indices r, the latter identity yields another interesting formula:
(23) 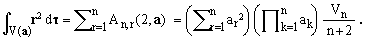
5. Volumes of n-dimensional ellipsoids and spheres
When all the p's are zero, Eq.(17) gives simply the volume of an ellipsoid whose main axes are specified by the set a. Explicitly, this turns out to be
(24) 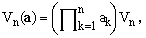
showing that the the numbers Vn of Eq.(22) are the volumes of n-dimensional spheres of unit radius. Their values can be easily calculated by means of the recurrence
(25) 
The volume of an n-dimensional ellipsoid has the dimension of the n-th power of length. This coincides with the popular notion of "volume" only in the case of n=3 but its extension to any n is quite obvious. In particular, for n=2 it coincides with the common concept of "area" of an ellipse and for n=1 with the "length" of a 1D-interval. The value of 1 for n=0, implicit in the above recurrence relations, might be considered as the cardinality of a set of a single 0D point.
Volumes and other volume integrals for n-dimensional spheres with unit radius
| |
| Dim |
Volume |
|
Volume integral of: |
| symbolic |
numeric |
|
|x1| |
x12 |
r2 |
|x1x2| |
x12x22 or x14/3 |
r4 |
| |
| 1 |
2 |
2.000000.. |
|
1 |
2/3 |
2/3 |
- |
- |
2/5 |
| 2 |
π |
3.141592.. |
|
4/3 |
π/4 |
π/2 |
1/2 |
π/24 |
π/3 |
| 3 |
4π/3 |
4.188790.. |
|
π/2 |
4π/15 |
4π/5 |
8/15 |
4π/105 |
4π/7 |
| 4 |
π2/2 |
4.934802.. |
|
8π/15 |
π2/12 |
π2/3 |
π/6 |
π2/96 |
π2/4 |
| 5 |
8π2/15 |
5.263789.. |
|
π2/6 |
8π2/105 |
8π2/21 |
16π/105 |
8π2/945 |
8π2/27 |
| 6 |
π3/6 |
5.167712.. |
|
16π2/105 |
π3/48 |
π3/8 |
π2/24 |
π3/480 |
π3/10 |
| 7 |
16π3/105 |
4.724765.. |
|
π3/24 |
16π3/945 |
16π3/135 |
32π2/945 |
16π3/10395 |
16π3/165 |
| 8 |
π4/24 |
4.058712.. |
|
32π3/945 |
π4/240 |
π4/30 |
π3/120 |
π4/2880 |
π4/36 |
| 9 |
32π4/945 |
3.298508.. |
|
π4/120 |
32π4/10395 |
32π4/1155 |
64π3/10395 |
32π4/135135 |
32π4/1365 |
| 10 |
π5/120 |
2.550164.. |
|
64π4/10395 |
π5/1440 |
π5/144 |
π4/720 |
π5/20160 |
π5/168 |
| |
6. Asymptotic behavior
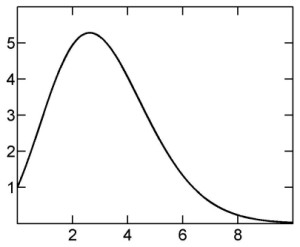 Equation (22) for the volume of an n-dimensional sphere of unit radius can be rewritten in terms of the following function ν(x):
Equation (22) for the volume of an n-dimensional sphere of unit radius can be rewritten in terms of the following function ν(x):
(26) 
The graph of ν(x) is shown on the right. It is evident that it passes through a maximum and then, for x growing to infinity, decays to zero. The rate of the decay for large values of n can be estimated using the Stirling approximation [4,5] for Γ(x), but the result is not particularly enlighting. What it shows is the validity of the following limit
(27) 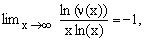
indicating that, for very large x, the decay is dominated by a factor of the form O[x-x].
|