|
There is an approximation to ellipse perimeters which has an interesting history.
Using the symbolism and terminology of Sykora's 2005 Review (hence just R), it is
(E5) 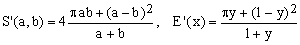
and its maximum error is 0.631%. In a 2006 addendum to his review, Stan Sykora wrote:
When writing my first article on ellipse perimeters, I was convinced that (R:E5) was quite original. Soon after the article went online, however, I have found out that the formula matches the first term of D.F.Rivera's approximation (R:C3). I have therefore amended the article with a note to that effect and, in the Review, coined the term Sykora-Rivera approximation. Then, reading the article and the Review, David Cantrell realized that an earlier expression of his which he called particularly fruitful, though written differently, is identical to mine and Rivera's. Mentioning the fact to me, he added: "I doubt that I am the first person to have suggested using (R:E5) to approximate the perimeter of an ellipse. It's such a simple approximation that it was probably suggested long ago by someone else. But who?"
We have recently found at least a partial answer to D.Cantrell's question. The formula is mentioned in an Editor's footnote to a Hungarian 1980 edition of a Mathematical Pocketbook by I.N.Bronshtein and K.A.Szemendyayev (see the pertinent page). The Editor refers to a 1954 article in Zeitschrift für Angewandte Mathematik und Mechanik (now Journal of Applied Mathematics and Mechanics) and sets its maximum error to < 0.7% (the more precise value is 0.631%).
In the latter article [1], Morris D.N. and Smith J.W. propose the approximation as an original one (see the pertinent excerpt) and compare it with three other approximations (though numeric values are not given). In view of this, perhaps the approximation should be renamed again and referred to as Morris-Smith's. However, since the article is dedicated to a quite different topic, it does not appear that they have researched prior literature enough to make sure they were not re-discovering (rather than discovering) the formula, just like the three would-be discoverers after them (Rivera, Cantrell, Sykora). Their only reference to ellipse perimeters is to an engineer's handbook [2]. It is therefore wise to stick to David Cantrell's proposal and call it just the Particularly Fruitful approximation.
The two sources mentioned above refer to several other approximations to ellipse perimeter. The first one is in both cases identical with Peano's [R:K4] and the second one in ref.[1] is identical to Padé 2/1 [R:Kc, known also as Hudson-Lipka]. The second approximation listed in ref.[2] has not yet appeared anywhere in this series [4] of articles, but it is listed also in [3]. It combines in a simple way the arithmetic and quadratic means of the ellipse axes and, attaining its maximum error of about 5.2% at b/a = 0, belongs to the class of Keplerian approximations [R]. For completeness sake, we list it here as K13:
(K13) 
The third formula listed in reference [2] is not symmetric under exchange of (a,b) and therefore is of no interest here.
|