|
The classical Antenna Reciprocity Theorem
In classical treatises on electromagnetic fields [9] and antennas [8], the antenna theorem is usually formulated as follows:
Given two antennas A and B placed at some distance, each of them can be operated either as a transmitting antenna or as a receiving antenna. Suppose that antenna B is kept intact, while the performance of antenna A as a transmitter is modified so that, for a fixed amount of input power, the signal received by antenna B changes by a factor F. Then the same modification changes also the performance of antenna A as a receiver and does so by the same factor F.
The theorem follows from certain symmetries of Maxwell equations and its validity is easily verified experimentally.
Adaptation to Magnetic Resonance
In magnetic resonance the signal is normally detected using what at first sight appears as an induction [1] coil (NMR, MRI) or a resonant cavity (ESR). However, this description presents conceptual problems [5] since classical induction can not account for the evidently quantum character of MR spectra which implies absorption and emission events involving discrete electromagnetic quanta. Especially in the case of nuclear magnetic resonance (NMR) and imaging (MRI), where one uses induction coils and there is no detectable radiation exiting/entering the sample area, the quantum nature of the phenomenon is not easy to reconcile with classical Faraday induction.
Fortunately, it is clear that the interaction energy E between a magnetic moment m of a particle and a magnetic field B is described by the same formula (E = - m.B) in both the classical and the quantum formalism. Consequently, it is this term which plays a key role in resolving the apparent impasse. Since the way how this works out is too long to follow here, let us see right away the result for the radiation-less case of transmitter/receiver coils. The modified theorem, which we might also call the MR reciprocity law, applies to all devices capable of both producing magnetic fields and detecting MR signals (simple loops, solenoids, saddle coils, bird-cage coils, multi-coil assemblies and, as a limit case, cavities):
The sensitivity of a magnetic resonance assembly, used as a receiver, to nuclides present at a point X is proportional to that assembly's efficiency, when used as a transmitter, to generate at that same location X a radiofrequency field B1.
The efficiency of the assembly is measured by the amplitude of B1 produced using a fixed input power P. More precisely, what matters is the component of B1 which is transversal to the main field B0, but the orthogonality of B1 and B0 should be guaranteed by the geometry of the design.
One great merit of the theorem is that it makes superfluous the old and irrational concept of coil filling factor [1,2]. Consider, for example, a simple loop like the one in Figure 1 and suppose that we use it as a transmitter to generate an RF magnetic field at point X. When the coil is tuned and matched so that the whole assembly has a predefined impedance Z0 (usually 50 Ω), a fixed power P implies a fixed current J. Suppose now that we reduce the diameter of the loop by a factor F and retune it again to Z0. Then, at input power P, we have still the same current J but, according to the Biot-Savart law [9], the generated magnetic field B1 is greater than before by the factor F. Consequently, according to the Theorem, the sensitivity of the smaller coil to a nuclide present at X will be F times that of the larger coil.
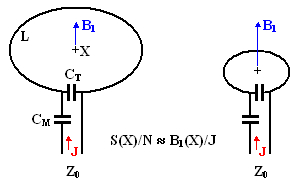
Figure 1. Illustration of the NMR Antenna Reciprocity Law.
The sensitivity of a front-end assembly at a point X is proportional to the RF field it generates therein when used as a transmitter and fed a pre-defined power. For the test, the input impedance and the current must be kept constant and the assembly must be tuned to the Larmor frequency of the observed nuclides. As always, B1 must be perpendicular to the main magnetic field B0.
The above discussion makes sense since it relates the sensitivity of an assembly (inclusive of its tuning and matching circuitry) at a point X to its capability to produce at X a magnetic field when used as an RF field generator rather than a sensor. This combines geometric and electric characteristics of the assembly with the relative location of X - all features which clearly need to be taken into account when talking, for example, about sensitivity to small voxels inside a large MRI coil (notice that in such cases the concept of a 'filling factor' is not applicable at all). It can be shown that the sensitivity to nuclides present at a point X is proportional to
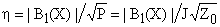 , ,
where B1(X) is the RF field produced at X when the assembly is used as a transmitter and fed the power P.
One important and easy to remember corollary of the theorem is the relation between sensitivity and the width of 90o excitation pulse. Since the latter is inversely proportional to the B1 magnitude, it follows that:
If a modification of the front-end assembly shortens by a factor F the duration of the 90-degrees pulse, with no change in the employed RF power, the sensitivity of that assembly increases by the same factor F.
Applications
Microcoils for NMR spectroscopy
It was shown above that when an assembly is linearly scaled down by a factor F, its inherent sensitivity increases by F. Its volume, of course, decreases even faster (F^2 when just two dimensions are scaled), but that needs not be a problem when the sample itself is tiny. A more serious limit is represented by technical problems such as the fact that when the assembly size decreases, it becomes increasingly difficult to tune it and to maintain a reasonable Q-factor. In NMR spectroscopy, another drawback is also the progressive loss of homogeneity due to susceptibility effects.
Inductively coupled MRI coils
Consider now the situation shown schematically in Figure 2. When a passive, tuned loop is inserted into a larger, primary coil, the two coils become inductively coupled. When the assembly is used for transmission, the value of the generated RF field at some point X can be much higher in the two-coils configuration (right) than in the single-coil version (left). Consequently, the configuration with two inductively coupled coils, when properly designed, may have a higher sensitivity (on the other hand, it has necessarily a smaller field of view).

Figure 2. The principle of inductively coupled multi-coil front-end designs.
When a smaller, tuned coil B is inserted inside a single-coil assembly A, the field generated inside B during transmission can increase by a considerable factor. According to the reciprocity theorem, this boosts by the same factor the sensitivity of the assembly, when used as a receiver, for nuclides present inside the smaller coil. Notice that the smaller coil may change not only the magnitude but also the direction of the B1 field vector (only the component perpendicular to B0 is pertinent to our discussion).
This, plus the fact that induction permits to 'extract' a signal without any physical contact, is the principle behind many inductively coupled coil designs [7] used mostly in MRI.
Inductively coupled coils for MAS
The mechanical independence of inductively coupled coils makes it possible to rotate one, while the other is fixed. This has recently led to the discovery [10] of a novel type of highly sensitive magic angle spinning two-coil assemblies.
See my blog entry for more details about these devices.
A final reflection
In my opinion, the reciprocity theorem has not yet received by the NMR community all the attention it merits and we can expect more surprises like the Sakellariou MACS rotor discovered [10] this year.
I fully agree with David Hoult [5] that the MR phenomenon is not purely inductive in nature (only one of the many different ways to detect MR signals uses classical induction coils). In this sense, paradoxically, Felix Bloch might have done a disservice to magnetic resonance when he chose the title Nuclear Induction for his pioneering paper [1]. Ever since, there was so much attention focused on 'The Coil' that it might have obscured the true, quantum nature of the coupling between a nuclide and the front-end sensor [11].
There is, of course, a relation between the latter coupling and classical induction. The problem is that if we want to explain the spectral characteristics of MR signals we absolutely can't do without quantum mechanics, but there is no coherent quantum description of the classical induction phenomenon. It is understood that by applying the formalism of quantum electrodynamics one should be able, in principle, to model also classical induction. While there is no reason to doubt this, it has never been carried all the way through. As a result, we use two totally different descriptions of the MR phenomena: quantum and classical, choosing empirically the one which appears to match best the experimental phenomenon at hand. This situation is most unsatisfactory and a great merit is due to David Hoult for having found the courage to face the fact. Alas, he was not [yet] listened to with a due attention.
|