|
Introduction
Consider the set of n-tuples of distinct objects, each of which can exist in two states labelled "0" and "1". A possible example consists of n-tuples of spin-1/2 particles with their two spin states. Those who prefer to avoid such physics jargon, however, may consider the binary-coded n-bit integers with their binary digits.
Let Q(x), or the Q-state of x, be the number of objects in an n-tuple x which are labelled "1".
Examples: Q({0011010}) = 3, Q({1110011}) = 5.
Now consider the set T of pairs [x,x'] of n-tuples. We will call such pairs transitions. We will further narrow our attention to subsets Tp of T containing just the so-called p-quantum transitions for which Q(x')-Q(x) = p, where 0 ≤ p ≤ n.
Example: [{0011010},{1110011}] is a 2-quantum transition.
We will prove that the total number of possible p-quantum transitions N(n,p) is equal to
(1) 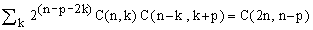 , ,
where p is any constant integer and C(n,k) is the binomial coefficient (number of ways of choosing k elements out of n distinct ones), assumed to be null whenever k < 0 or k > n. Though the summation extends formally over all k, only a finite number of terms is non-zero. Likewise, while p may be any integer, the cases for which the two sides of the identity are not zero are limited to 0 ≤ p ≤ n.
Equation (1) has here a dual significance: first, it is an answer to out physical problem of determining N(n,p) and, second, it is a generic combinatorial identity.
Example: for n = 4 and p = 2 we have N(4,2) = 2^2 C(4,0)C(4,2)+2^0 C(4,1)C(3,3) = 4.1.6+1.4.1 = 28 = C(8,2) so that in a coupled system of 4 spin-1/2 particles there are 28 double-quantum transitions.
Proof
Method 1: By definition, if x is any n-tuple with Q-state q then x' must have the Q-state q+p.
Since there are C(n,q) n-tuples x with Q(x) = q and C(n,q+p) n-tuples with Q(x) = q+p, we have
(2) 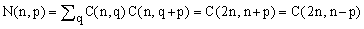 , ,
where the second equality is a special case of the following well-known [ref.1] combinatorial identity
(3) 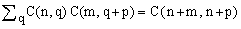 , ,
and the last equality follows from C(m,k) = C(m,m-k).
Method 2: For every generic p-quantum transition there exists a natural number k such that k objects change from "1" to "0",
k+p objects change from "0" to "1" and the remaining 2k+p objects do not change.
Let us call this unique k the combination index of the transition.
The number of ways to construct a p-quantum transition with a combination index k is the product of three factors:
C(n,k) ways of choosing the objects which change from "1" to "0",
C(n-k,k+p) ways to choose among the remaining objects those which change from "0" to "1", and
2^(n-2k-p) possible states of those objects which do not change.
Hence, since the combination indices partition the set of p-quantum transitions into disjoint subsets,
(4) 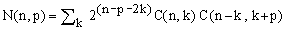 . .
Comparing (2) and (4), one obtains (1).
Physical significance
A typical theoretical problem of Nuclear Magnetic Resonance (NMR) spectroscopy is the time-evolution of a system of n coupled spins. This requires quantum mechanics and the most rigorous approach to the problem is using the Liouville space formalism. Liouville space is a linear vector space of the Hilbert type constructed above a basis which includes all quantum state transitions. In NMR, the Liouville space is finite-dimensional but the number of dimensions may be huge. For example, the complete Liouville space of a system containing 8 particles with spin 1/2 has a base with 4^8 = 65536 elements and its rigorous handling would require the manipulation of 65536 x 65536 matrices!
In a freely evolving system the full Liouville-space evolution matrix factorizes according to the p-quantum transitions - subspaces belonging to different p's evolve in an essentially independent way (at least when relaxation effects can be neglected). In 'normal' single-quantum NMR one needs to consider only the subspace belonging to p = 1 with dimension is N(n,1). In our example of n = 8, this evaluates to 'just' 11440.
Further reduction is achieved considering that transitions with combination index k = 1 are much weaker than the main transitions with k = 0 and the intensities of combination transitions with k > 1 are absolutely negligible. This means that, to an excellent approximation, the summation in equation (4) can be truncated at k=1 or even at k = 0 when strong couplings are not an issue. In our case of n = 8 this leads to reduced Liouville space dimensions of 8192 and 1024, respectively. Matrices of this rank, though still quite large, are already manageable.
A comment on combinatorial identities
At the time I have formulated the identity (1) and the above proof, I thought that it was rather original and presented it to the Google sci.math group. I was kind of rebuked and invited to read the book A = B by Petkovsek, Wilf and Zeilberger for a universal way of proving such combinatorial identities, based on the Sister Celine method, expressions for combinatorial coefficients in terms of hypergeometric series, and recursive formulae for the latter. The approach is compatible with automatic execution by computers and makes part of the Mathematica package which, in a certain sense, preempts all originality claims regarding any future combinatorial identity and gives rise to a relatively well-justified conviction that any combinatorial conjecture can be proved right or wrong in a 'mechanical' manner.
At the time I felt a bit ashamed of not being aware of the book, so I did not argue the case. Today, I agree that publishing combinatorial identities for the mere sake of doing so is no longer a meritorious activity. On the other hand, I can't help but feel that this somehow removes much of the fun from the respective math. An application-based, human proof like the one above has a more convincing quality and leaves one with a satisfaction much superior to a sterile machine proof.
The issue, in my opinion, goes beyond mere subjective pleasure. Application-oriented proofs of combinatorial identities are often of considerable educational value and they are in most cases easily accessible at college and sophomore levels.
This, I believe, is by itself an important point in their favor.
I also find one important aspect lacking in a machine proof of a mathematical statement: the proof can be carried out only after the statement has been formulated, but it does not help at all with the formulation itself. In the present case, for example, we have derived two apparently different combinatorial formulas for the number of p-quantum transitions in a system of n spin-1/2 particles and thus proved their identity. The techniques of the A = B book provide an alternative way of proving the identity of the two formulas, but they can't contribute to the understanding of what each of them means in a specific context.
My present position is that it is very nice and useful to have a universal tool for proving a certain category of theorems or conjectures, but it does not make it any easier to formulate them and to exemplify their meaning.
|