Introduction

Multidimensional NMR spectroscopy has expanded dramatically in recent years and is now considered the most powerful tool for the study of structure, dynamics, and interactions of both low molecular weight compounds and biomolecules. Among the many 2D NMR experiments, the so-called homonuclear experiments are characterized by having diagonal peaks which merely provide the same information as the conventional 1D experiment and cross peaks which are the important diagnostic feature. It is not uncommon that the diagonal obscures close cross peaks so removing it will facilitate a more accurate analysis of the 2D NMR experiment of interest. Different approaches to obtain diagonal-free 2D NMR spectra have been recently reported ranging from modifications of the pulse sequences [1] to post processing techniques [2].

Modifications of the pulse sequences require more complicated acquisitions schemes and often decrease the experiment sensitivity. On the other hand, post processing methods, usually accomplished by means of modified high-pass frequency convolution filters, often distort peak intensities and baseline close to the diagonal peaks. Recently, the Wavelet Transform has been proved to be extremely effective to the suppression of on-resonance solvent signals satisfying two fundamental criteria [4]:

• Selectivity: The width of the suppressed signal can be adjusted so that the peaks close to it are recovered without peak distortion of the peak shape and intensity
• High computational performance

In this application note, we will show that the Wavelet Transform can be used as an efficient method for the removal of diagonal peaks in 2D homonuclear NMR experiments. The effectiveness of the scheme is demonstrated by applying the method to remove the diagonal of a phase-sensitive TOCSY spectrum of Strychnine.

Discussion

Similarly to numeric solvent subtraction techniques, our proposed algorithm is designed to suppress on-resonance signals, i.e. those at the centre of the spectrum.

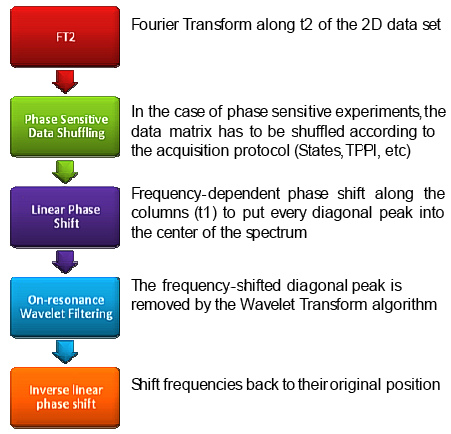Figure 1. Flow chart of the new algorithm.
 

The overall algorithm is depicted in Figure 1 which follows essentially the same logic described in [3] but with the significant introduction of the Wavelet Transform in place of the convolution filter previously reported by Marion et al [5]. Such high pass filter may introduce distortions at the head and tail of the time-domain data, often characterized in the frequency domain spectrum by a "hump" close the diagonal. Fiedrichs et al. [3] proposed to use a variable window length for the convolution kernel so that it is a function of the position of the point to be filtered. However, the band width of this filter becomes very large for the first few points in the FID, causing strong attenuation in spectra where the first points, unlike phase-sensitive COSY, are not initially small. Another approach would be to multiply the FID, once the filter has been applied, by a suitable window function which attenuates the first points in the FID. Again, this method is not efficient in those experiments in which the intensities of the first points in the t1-FID are important. Our Wavelet-based method does not suffer from these limitations and as a result, it can be applied to any 2D NMR spectra.

Thus, our method consists in temporarily shifting columns of a 2D spectrum in such a way that the diagonal signal is moved to the centre which is then suppressed by the Wavelet filter. So once the spectrum has been Fourier transformed along the acquisition dimension (t2), a frequency-dependent phase shift along every column (t1) is applied to put every diagonal signal into the centre of the spectrum. This procedure is simply a first order phase correction in the time domain. Next, the frequency-shifted diagonal peak is removed by the Wavelet Transform algorithm (described below) and lastly, the frequencies are shifted back to their original position.

The Wavelet Transform

The Wavelet Transform decomposes a signal f over wavelet functions obtained as translations u and dilations s of a mother wavelet function y of zero average:

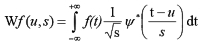
Sampling the translation and scale parameters as u=2jn and s=2j, it is possible to construct a discrete orthogonal wavelet basis holding the signal details necessary to obtain a finer resolution representation of the signal, which is related with a multi-resolution representation (MR).

The procedure of MR is illustrated below, where Cj and Dj are called, respectively, the discrete approximation and the discrete detail, H and G are discrete filters for the transformation process.

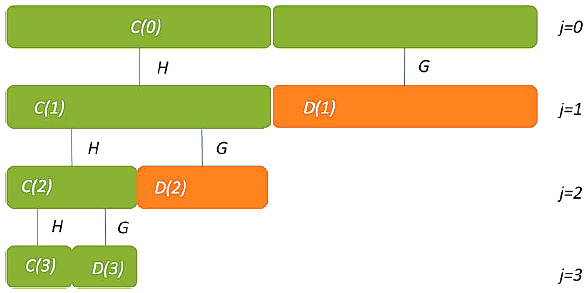
Figure 2. Diagram showing the operation of the multiresolution decomposition method.
Green segments represent the coefficients to be stored
 

On resonance filtering

The process of on-resonance filtering via multi-resolution decomposition can be summarized as follows:

• A mirror image t1-FID is calculated to avoid edge effects.
• The t1-FID is decomposed by the WT into 2Jmax dyadic levels (where Jmax = log2(N),
  N being the number of points in the t1-FID
• The points corresponding to low frequencies are zeroed
• The original FID is reconstructed by applying an inverse WT

Results

To demonstrate the utility of this procedure, we have recorded a TOCSY spectrum of strychnine consisting in 1024 x 128 data points. The spectrum was Fourier Transformed along the direct dimension to have a final size of 1024 complex data points and zero filled along t1 to yield a final data matrix of 1024 x 1024 complex data points. Therefore, the maximum number of Dyadic levels is 10.

In all the examples shown below, the Daubechies wavelet filters with 12 coefficients have been used.

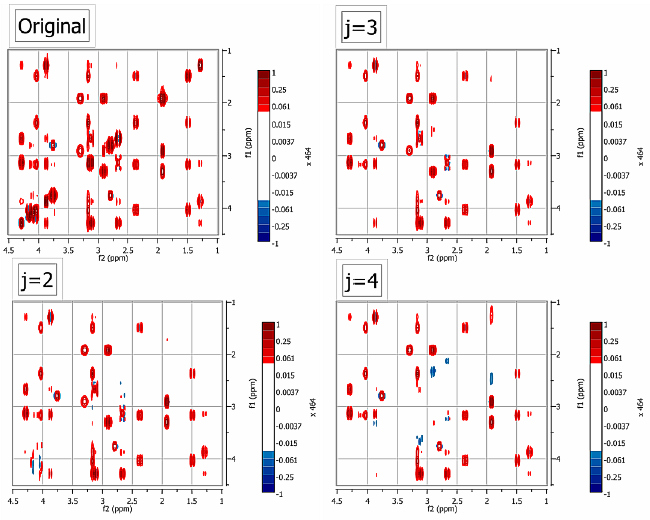
Figure 3. Example of the application of the new algorithm to a TOCSY spectrum of strychnine
 

In Figure 3, the diagonal was suppressed after leaving out the first 2, 3 and 4 dyadic levels using a Daubechies-12 Wavelet. It can be appreciated that as the number of removed dyadic levels increases, the selectivity of the filter decreases. By selecting the appropriate number of dyadic levels (2 in this case), the diagonal can be effectively removed without affecting the nearby cross peaks.

The superior selectivity of the Wavelet filter ad the ability to work with dispersive signals are demonstrated in the figure below. A series of antiphase signals (7 Hz coupling) was generated using Mnova (Figure 4A). In Figure 4B the on-resonance signal was suppressed using a convolution filter with a width of 64 points. It can be appreciated that signals close to the 0 Hz peak are attenuated by greater than 30%. The distortions caused by this filter to neighboring peaks can be reduced by increasing the number of points of the convolution function. However, this will also lead to a lower attenuation of the diagonal signals.

Figure 4C depicts the sharpness of the edge of the Wavelet filter (Daubechies-12, eliminating 10 dyadic levels, being 12 the maximum number allowed). The central signal is efficiently suppressed without any distortion of other signals.

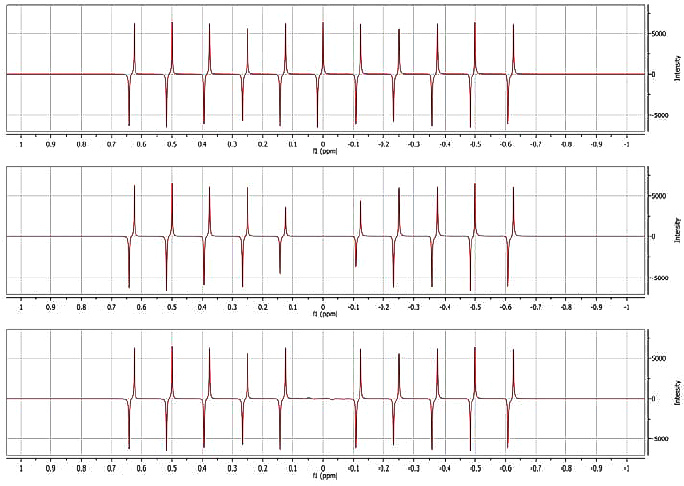
Figure 4. Result of applying the wavelet filter to suppress an antiphase peak
 

Conclusion

In summary, we have shown that undesirable diagonal peaks can efficiently be removed by the proposed wavelet based filtering technique. The main advantages of the proposed algorithm are:

• It makes it possible to recover diagonal signals which are close to the diagonal.
• It can be applied to suppress strong diagonal peaks in COSY, TOCSY, NOESY, ROESY and other correlation spectra.
• Unlike time domain high pass filters, it does not distort the first points of the FID.
• It is computationally very efficient.