|
Introduction and definitions
Consider an n-tuple of positive real numbers a ≡ {ak}, k=1,2,...,n.
We will use the terms linear sum of ratios and cyclic sum of ratios, respectively, for the the following expressions Ln(a) and Cn(a):
(1) 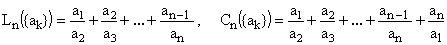 . .
It turns out that these expressions satisfy inequalities which are a generalization of the following special cases
(2) 
which are easily proved using elementary analysis.
The linear-sum-of-ratios inequality
We will first postulate the inequality for the general case of Ln and then prove it by induction:
(3) 
For simplicity, we have dropped the argument of Ln - a convention which will be henceforth followed (hopefully, this will not give rise to any confusion).
For n = 2, the statement holds. Let us assume that it holds for some n and see whether it then holds also for (n+1).
We have
(4) 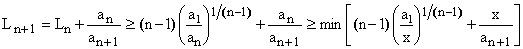
The unique minimum (with respect to x) of the right-hand side expression is again easily determined by elementary analysis.
It occurs for
(5) 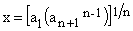
and its value is
(6) 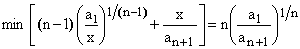
in accordance with (3). Hence, inequality (3) is proved.
The cyclic-sum-of-ratios inequality
The cyclic sum of ratios Cn is identical to Ln+1 with an+1 = a1. Applying (3), we therefore have
(7) 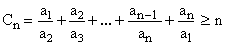
Equality conditions
A remarkable feature of the inequality (3) consists in the fact that its right-hand side depends only upon the ration between the first and the last element of the sequence (and, of course, upon the number of elements in the sequence a). In the cyclic case (7) this reduces further to just the number of elements. There is of course the legitimate question of whether, in both cases, the equality can occur and to which extent is it unique.
In the cyclic case, part of the answer is self-evident since to achieve equality, it is enough to set all the elements of a equal (though this does not yet prove uniqueness). In the general case, one should first notice that (3) and (7) remain invariant when all elements of a are multiplied by any positive constant factor. Such a scaling needs to be taken into account when discussing uniqueness of equality solutions.
The strongest indication with regard to equality comes from the recurrence process we have used to prove the inequality and, in particular, from (4) and (5). Evidently, an equality in each of the recursive steps is both a sufficient and a necesary condition of equality in the final expression. This means that, for any k, we must have
(8) 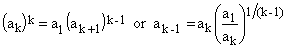
For Ln, given any values of a1 and an, the last formula can be applied recursively starting from k = n and proceeding down to k = 2 (for which it reduces to the trivial identity a1 = a1). In other words, a1 and an can be set arbitrarily but, once defined, all the intermediate elements of a need to have uniquely defined values in order to produce an equality in (3).
Since Cn can be viewed as Ln+1 with an+1 = a1, the recursion (8) gives us the expected equality 'solution' with all ak equal to a1 and guarantees that it is unique up to the arbitrary choice of a1).
Functional extensions
The inequalities (3) and (7) can be used to derive others by means of functional transformations. While most such cases are either trivial of relatively uninteresting, one particular case leads to a rather elegant inequality.
Let {xk}, k=1,2,...,n , be an n-tuple of real numbers (not necessarily positive). Define now an n-tuple of positive numbers {ak} by setting, for every k, ak = exp(xk). Applying (3) and (7) to the the latter n-tuple and then expressing the a's in terms of the x's, one obtains
(9) 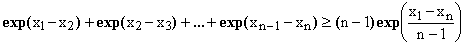
(10) 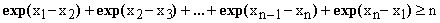 . .
Inequality (9) answers the problem of distributing (n+1) cut-points within an interval (such as [0,1]) so as to minimize the sum of exp(-Δk) running over all the n resulting sub-intervals Δk = xk+1 - xk. The optimal cut-point positions (see recurrence 8), as well as the value of the sum's minimum (in our case n.exp(-1/n)) can now be easily determined and turn out to correspond to a uniform cut-points distribution with all intervals having the same length. Naturally, this result could be obtained just as well by variational calculus; the present approach is just an alternative.
An application
It is probably improper to talk about applications when it comes to generic inequalities, since the occasions where they can be profitably used are infinite. However, I have been propelled into studying this topic while tackling a class of non-linear multivariate fitting and it is perhaps proper to make a comment on this context.
Benchtests for multivariate minimum-search or optimization algorithms
Inequalities (3) and (9) can be used as non-trivial cases for testing and performance analysis of minimization and optimization algorithms. It is sufficient to fix a1 and an (or a1 and an), consider the remaining n-2 elements as adjustable variables (or parameters) and, after assigning them some arbitrary starting values, use a numeric algorithm to minimize Ln. The advantages are:
- Ln is known to have a unique minimum,
- the values of the variables for which the minimum is obtained are a-priori known,
- the exact value of the minimum is also known,
- the dimensionality of the problem (number of variables) can be set to any value,
- the problem is far fom linear,
- there is a pronounced interdependence (coupling) between the variables, and
- by making the ratio an/a1 very large (e.g. 10^5), the optimal parameters can be made to differ by orders of magnitude.
The latter three points can be used to make sure that, whatever is the tested algorithm, it gets quite taxed.
Addenda
Added on November 13, 2009:
There is a simple alternative proof of the inequality (3), based on the fact that - for any set a of non-negative real numbers - the geometric mean never exceeds the arithmetic one. In (3), the left-hand side, divided by (n-1) is the arithmetic mean of all the consecutive ratios, while the right-hand side, again divided by (n-1), is their geometric mean. Hence the inequality. Equality, as known, occurs only iff all the terms of the two means are equal, i.e., when all the ratios are the same.
|