Introduction

Let [xl,yl], [xc,yc] and [xu,yu] be three points of a real function y(x) of real variable x (see the Figure). Here the specifier characters l, c and u stand for lower, central, and upper, respectively. However, the code listed below and the formulae on which it is based are actually invariant under the reversal of the order of the three points, so that the only requirements are that xc should lie in the interval between xl and xu and that it must not coincide with any of the two border values. There are no restrictions on the y-values yl, yc and yu.

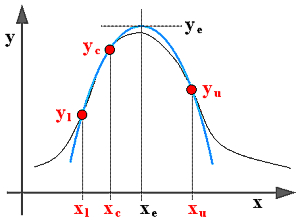
Figure legend: The three input points are shown in red. The quadratic function passing through them is the thick blue parabola. The thin black curve is a schematic representation of an actual function y(x) which, obviously, need not match the quadratic approximation. Also shown are the position and the value of the quadratic approximation extreme (in this case a maximum).

In general, the three x-values do not need to be spaced evenly (xc-xl may differ from xu-xc). However, a uniform distribution of points is a very common special case (especially when handling tabulated functions) and so is the even more special case when the distance between any two consecutive points is assumed to be 1 (numbered data points). These special cases are covered by appending _e (evenly spaced, meaning that xc-xl = xu-xc = d) or _1 (xc-xl = xu-xc = 1) to the function names.

The considered quadratic approximation is of the type

(1)  y(x) = (d2/2)*(x-xc)^2 + d1*(x-xc)+ d0,

where d0, d1, d2 are the zeroth, the first and the second derivative, respectively, whose values are determined indirectly by the condition that y(x) must pass through the three "input" points, i.e.,

(2)  y(xc) = yc, y(xl) = yl, y(xu) = yu.

We will use throuhout the type REAL. Usually, this will be a double or a float; the User may establish the equivalence either by means of a #define or by a typedef statement.

The derivatives

Applied to Eqs.(2), elementary algebra gives the following formulas:

(3)  d2 = 2 ([(yu-yc)/(xu-xc)] - [(yc-yl)/(xc-xl)]) / (xu-xl),
      d1 = [(yu-yc)/(xu-xc)] - (d2/2)(xu-xc) = [(yc-yl)/(xc-xl)] + (d2/2)(xc-xl),
      d0 = yc

As anticipated, we assume that neither of the values (xu-xc), (xc-xl) and (xu-xl) is zero (no test of the condition is done). In an application, this usually follows from the context; otherwise, one must implement suitable independent tests before calling the functions listed below. Since there are two numerically different forms for d1, one should use the more precise one which is the first when xu-xc > xc-xl and the second one otherwise (the choice becomes irrelevant when the spacing is uniform). The following functions calculate and return the derivatives d1 and d2 (there is no need to calculate d0 which is trivial):

REAL P3InterpolateDer(REAL xl,REAL xc,REAL xu,REAL yl,REAL yc,REAL yu,REAL &d1)
// -----------------------------------------------------------------------------------------
// Optimized calculation of the derivatives d1 and returns d2
// (d2 is the return value, and d1 is set as a side action)
{
  REAL d2 = 2*((yu-yc)/(xu-xc)-(yl-yc)/(xl-xc))/(xu-xl);
  if ((xu+xl)>=(xc+xc))
     d1 = (yu-yc)/(xu-xc) - 0.5*d2*(xu-xc);
  else
     d1 = (yc-yl)/(xc-xl) + 0.5*d2*(xc-xl);
  return d2;
}
 
REAL P3InterpolateDer_e(REAL d,REAL yl,REAL yc,REAL yu,REAL &d1)
// -----------------------------------------------------------------------------------------
// Calculates the derivatives for the equidistant case when xl=xc-d and xu=xc+d
{
  REAL d2 = (yu-yc+yl-yc)/d/d;
  d1 = 0.5*(yu-yl)/d;
  return d2;
}
 
REAL P3InterpolateDer_1(REAL yl,REAL yc,REAL yu,REAL &d1)
// -----------------------------------------------------------------------------------------
// Calculates the derivatives for the equidistant case when xl=xc-1 and xu=xc+1
{
  REAL d2 = yu-yc+yl-yc;
  d1 = 0.5*(yu-yl);
  return d2;
}

In all cases, the return value is the 2nd derivative which is probably the most useful datum;
the 1st derivative is returned through the referenced arguments.

Interpolation/Extrapolation

Using Eq.(1) and knowing the derivatives, it is easy to calculate the interpolated/extrapolated value y(x) for any x:

REAL P3Interpolate(REAL x, REAL xc,REAL yc,REAL d1,REAL d2)
// -----------------------------------------------------------------------------------------
// Calculates y(x) using the values of xc,yc,d1 and d2
{
  REAL dx = x-xc;
  return yc + dx*(d1+0.5*d2*dx);
}

Warning: As evident from the Figure, the quadratic approximation is generally inappropriate for numeric extrapolation, i.e., those cases where x lies outside the interval [xl, xu].

In the case of irregularly spaced points [xl, xc, xu], the estimated function value of some importance may be the one corresponding to the center of the interval [xl,xu]. This is obtained simply by calling the function P3Interpolate with the argument x set to (xl+xu)/2.

Maximum/minimum and its location

Once the values d0 (=yc), d1, d2 are known, it is also easy to estimate from Eq.[1] the location and the value of the extremum:

(4)  xe = xc - d1/d2,   ye = yc - 0.5*d1*(d1/d2) = yc + 0.5*d1*(xe-xc).

The extremum exists when d2 is nonzero, in which case it is either a maximum (d2 < 0) or a minimum (d2 > 0). When the extremum lies too far outside of the interval [xl, xu], the estimated values of values xe, ye are numerically unreliable. By convention, we will flag it as unreliable when xe falls outside the interval [xl,xu], though this may be subject to discussion.

This is a straightforward implementation of Eq.(4) when the derivatives are already known:

REAL P3Interpolate_Extremum
      (REAL xl,REAL xc,REAL xu,REAL yc,REAL d1,REAL d2,REAL &xe,REAL &ye)
// -----------------------------------------------------------------------------------------
// Calculates the co-ordinates xe, ye of the extremum and returns
// the 2nd derivative d2 if the extremum is deemed reliable or 0.0 otherwise
// Negative return value indicates a valid maximum, positive return value a valid minimum.
// Zero return value indicates an unreliable extremum (this does not mean that d2 is zero).
// When d2 is exact zero, the function returns exact 0.0 in both xe and ye.
{
  if (d2) {
    xe = xc - d1/d2;
    ye = yc + 0.5*d1*(xe-xc);
  } else { // Degenerate d2
    xe = xc; // This could be NAN
    ye = yc; // This could be NAN
    return 0.0;
  }
  if ((xu>xe)||(xe<xl)) return 0.0; // Reliability test
  else return d2;
}

Here the estimated coordinates of the extremum are returned in xe and ye. When d2 is exact zero, xe and ye are made to coincide with the central point (an invalid NAN would be even better).
The value returned by the function can be one of the following:
   1) zero, indicating that the local maximum, if it exists at all, is too far outside to be reliable.
   2) negative 2nd derivative, indicating a valid local maximum,
   3) positive 2nd derivative, indication a valid local minimum,

Sometimes, the existence, the type, and the location of the extremum are the only desired information.
For that purpose it is best to use one of the following functions which determine the extremum starting from scratch:

REAL P3Interpolate_Extremum
      (REAL xl,REAL xc,REAL xu,REAL yl,REAL yc,REAL yu,REAL &xe,REAL &ye)
// -----------------------------------------------------------------------------------------
// Calculates the co-ordinates xe, ye of the extremum and returns
// the 2nd derivative d2 if the extremum is deemed reliable or 0.0 otherwise
// Negative return value indicates a valid maximum, positive return value a valid minimum.
// Zero return value indicates an unreliable extremum (this does not mean that d2 is zero).
// When d2 is exact zero, the function returns exact 0.0 in both xe and ye.
{
  REAL d1,d2;
  d2 = 2*((yu-yc)/(xu-xc)-(yl-yc)/(xl-xc))/(xu-xl);
  d1 = (yu-yc)/(xu-xc) - 0.5*d2*(xu-xc);
  if (d2) {
    xe = xc - d1/d2;
    ye = yc + 0.5*d1*(xe-xc);
  } else { // Degenerate d2
    xe = xc; // This could be NAN
    ye = yc; // This could be NAN
    return 0.0;
  }
  if ((xu>xe)||(xe<xl)) return 0.0; // Reliability test
  else return d2;
}
 
REAL P3Interpolate_Extremum_e
      (REAL xc,REAL d,REAL yl,REAL yc,REAL yu,REAL &xe,REAL &ye)
// -----------------------------------------------------------------------------------------
{
  REAL d1,d2;
  d2 = (yu-yc+yl-yc)/d/d;
  d1 = 0.5*(yu-yl)/d;
  if (d2) {
    xe = xc - d1/d2;
    ye = yc + 0.5*d1*(xe-xc);
  } else { // Degenerate d2
    xe = xc; // This could be NAN
    ye = yc; // This could be NAN
    return 0.0;
  }
  if (fabs(xc-xe)>d) return 0.0; // Reliability test
  else return d2;
}
 
REAL P3Interpolate_Extremum_1
      (REAL xc,REAL yl,REAL yc,REAL yu,REAL &xe,REAL &ye)
// -----------------------------------------------------------------------------------------
{
  REAL d1,d2;
  d2 = yu-yc+yl-yc;
  d1 = 0.5*(yu-yl);
  if (d2) {
    xe = xc - d1/d2;
    ye = yc + 0.5*d1*(xe-xc);
  } else { // Degenerate d2
    xe = xc; // This could be NAN
    ye = yc; // This could be NAN
    return 0.0;
  }
  if (fabs(xc-xe)>1) return 0.0; // Reliability test
  else return d2;
}

Use of global variables

Sometimes it is convenient to save xc, yc, d1, d2 in module-level static variables initialized by one of the following functions:

static REAL _xc = 0;
static REAL _yc = 0;
static REAL _d1 = 0;
static REAL _d2 = 0;
...
 
void P3Interpolate_Init(REAL xl,REAL xc,REAL xu,REAL yl,REAL yc,REAL yu)
// -----------------------------------------------------------------------------------------
{
  _xc = xc;
  _yc = yc;
  _d2 = P3Interpolate_Der(xl,xc,xu,yl,yc,yu,_d1);
}
 
void P3Interpolate_Init_e(REAL xc,REAL d,REAL yl,REAL yc,REAL yu)
// -----------------------------------------------------------------------------------------
{
  _xc = xc;
  _yc = yc;
  _d2 = P3InterpolateDer_e(d,yl,yc,yu,_d1);
}
 
void P3Interpolate_Init_1(REAL xc,REAL yl,REAL yc,REAL yu)
// -----------------------------------------------------------------------------------------
{
  _xc = xc;
  _yc = yc;
  _d2 = P3InterpolateDer_1(yl,yc,yu,_d1);
}

Once the values xc, yc, d1, d2 are stored in local variables, the interpolation function becomes more simple and looks like a trivial call of a real function of real variable:

REAL P3Interpolate(REAL x)
// -----------------------------------------------------------------------------------------
// Calculates y(x) using the previously initialized static values _xc,_yc,_d1 and _d2
{
  REAL dx = x-_xc;
  return _yc + dx*(_d1+0.5*_d2*dx);
}

The procedure, however, does not offer any advantage for the estimation of local extremum which requires the knowledge of all three X ordinates.

An alternative extremum reliability test

As anticipated, the line which tests for the extremum reliability is questionable in some contexts. An alternative which is more stringent than the one used above, and which may be especially useful in the cases of regular specing is to require xe to lie within half a step from xc. It gets encoded by one of the following lines (select just one):

  if (fabs(0.5*(xu-xl)*d2)<=fabs(d1)) return 0.0; // Generic reliability test
  if (fabs(d*d2)<=fabs(d1)) return 0.0; // _e Even-spacing reliability test
  if (fabs(d2)<=fabs(d1)) return 0.0; // _1 Spaced-by-1 reliability test

This is particularly useful when looking for local maxima in an array, since it will avoid picking up each maximum twice (once in two consecutive triplets).